The games newspeople play

 

                                            A winner or just a statistic? Photo credit: Britannica

Is Kamala Harris winning? The Washington Post and The New York Times would love to tell you. What they won't tell you is that they are either hopelessly confused or lying. 

Let's start with today's Post. "Vice President Kamala Harris holds a narrow lead over former President Donald Trump in the presidential election, a notable improvement for Democrats in a contest that a little more than a month ago showed President Joe Biden and Trump in a dead heat, according to a Washington Post-ABC News-Ipsos poll....Given the margin of error in this poll, which tests only national support, Harris's lead among registered voters is not considered statistically significant."

Big news, sports fans! Harris is winning! Our poll says so! But...wait a minute...it's not statistically significant, which means...um...hmm.

Friends and neighbors, you can't have it both ways. Either Harris is winning, or she isn't. The rule of thumb is this: If the poll margin is within the margin of error, you cannot deduce with 95% confidence that either Harris or Trump is winning. The race is a dead heat.

But.

Digging into the story, we learn from a graph that the poll has a margin of error of plus or minus 2.5%. Harris's lead in the poll is 4%, or 49% to 45%. So Harris is winning. The poll margin, 4%, is larger than the margin of error, 2.5%. It is statistically significant: In other words, the result is very likely to hold as well outside of the sample, for the country in general. The Post is breathtakingly mucked up.

Its confusion probably arises from its misunderstanding of the plus-or-minus designation. The idea is this: We want to test the hypothesis that the race is a tie. That would happen if Harris is neither winning nor losing. Our usual criterion is that we will accept that the race is a dead heat unless we are 95% confident that Harris is either winning or losing. Well, if Harris's lead exceeds 2.5%, it is not a dead heat. And had Trump's lead exceeded 2.5%, that is, had Harris's lead been -2.5%, it would not have been a dead heat. It is not the case that Harris's margin must exceed 2 times 2.5% for us to conclude that the poll result is statistically significant, that is, that the race is not a dead heat.

The further conclusion, that Harris is winning, is easy to confirm once we see that the race cannot be a tie. The intuition is this: If Harris is so far in the lead that we can reject the possibility that the race is a tie, then we can also reject the possibility that Trump is winning.

In this case, The Post lucked out. Its headline correctly said the poll indicated that Harris was winning. But there is a more important point: The Post doesn't know what the hell it is doing.

 The error about errors

 Newspapers goof when reporting polls because they do not understand how polling errors occur. When you ask someone in newspapers why they don't take the margin of error seriously, you will get an answer like this: Well, the pollsters told us they were careful about polling. So we didn't worry about potential errors. They had to be small. We reported the margin of error only because everyone says we should.  

Grrr.  Now hear this: The margin of error is calculated under the assumption that the polling was perfect. Even when the polling sample is an accurate mirror of likely voters, the outcome of the poll may not be accurate. There is still a good chance that too many Harris supporters were interviewed. There is also a good chance that too many Trump supporters were interviewed.

A simple example will show what I mean. Suppose that we have a class of 100 students: half receive As, and half receive Bs. (Welcome to grade inflation.) We take a sample of 10 students. Even if the sampling is utterly fair, there is still a chance that at least 6 of the 10 students sampled received As. Based on the sample, we wrongly conclude that the majority of students received As. In reality, only half did.

Because of such possibilities, statisticians test the idea that of all likely voters, half favor Trump and half favor Harris. We can dismiss this hypothesis of a dead heat if a large-enough share of the sample favors either Harris or Trump. The "margin of error" reflects how large the share of respondents backing one candidate must be if we are to dismiss the possibility of a dead heat, assuming perfect polling. If the pollsters made mistakes, and they usually do, the actual margin of error is even larger than the one usually reported.

Moving right along…

 For years, The New York Times has reported poll survey results as if they were true for likely voters in general. Yesterday's story is an example. Yes, we can conclude that Harris is leading in Arizona, because her margin (barely) exceeds the margin of error (see the figure below). But contrary to The Times, we cannot conclude with 95% confidence that either Harris or Trump is leading in North Carolina, Nevada, or Georgia. Those survey margins are within the margins of error, which are shown in the graph in the article. By the usual definitions in political polling, those races are dead heats.

Remarks later in the story indicate what The Times is really up to:  "As the Harris and Trump campaigns rush to define each other in the remade race, voters see a choice between strength and compassion. Voters were about equally likely to see each candidate as qualified and change-makers, but significantly more voters viewed Mr. Trump as a strong leader....When voters were asked who 'cares about people like me,' Ms. Harris had a slight edge over Mr. Trump: 52 percent compared to 48 percent."

The Times seems to think that it can report results from a sample as if they held for the population, as long as it labels results that hold with 95% confidence as "significant." (The poll margin for the question about strong leaders was 8%, much larger than the margin of error.) The Old Grey Lady is playing word games. Most readers are not statisticians. When The Times says Harris has "a slight edge," they think that The Times is talking about the population, that is, the world outside of the sample. They view the word "significantly" as redundant. 

So The Times has it both ways. It tricks readers into believing that it is breaking news by declaring a winner. And, if challenged, it can always point out that, after all, it did refer to significance, sort of.

A simple example will show why this is a cardinal sin. Suppose that the president of General Motors misstated stock earnings for years. The Securities and Exchange Commission would investigate and probably force the president to resign. He might even face charges of fraud. Shouldn't we hold the nation's leading newspapers to standards at least as high? In a close race like this, newspaper reports of the polls affect donors. The money is sloshing towards Harris because of her perceived momentum. How real is that perception?

Another common dodge of newspapers: Well, do we really need 95% confidence that Candidate X is winning? Surely 90% is good enough. In that case, the margin of error is smaller, and the poll margin may now exceed it.  We can then conclude that X is winning.

It is true that 95% is an arbitrary standard. But it is also a universal one, especially in political polling. To apply 95% in some cases and (quietly) 90% to others, which The Post is fond of doing, amounts to moving the goalposts at halftime for some games but not for others. It makes it hard to compare poll results. Is Harris ahead in certain polls because she is winning the race, or because those polls adjusted the margin of error until she was "winning"?       

The Times and The Post say their polling staffs have graduate training in statistics. I do not see how a well-trained statistician can unknowingly make errors this basic. I will leave it at that.  

Noncardinal sins....

There's more, much more. The Times writes: "The polls show some risk for Ms. Harris as she rallies Democrats to her cause, including that more registered voters view her as too liberal (43 percent) than those who say Mr. Trump is too conservative (33 percent)." 

It is not clear why The Times says this shows "some risk" for Harris. Perhaps it means that voters are significantly more likely to view Harris as liberal than to view Trump as conservative. If that's what it means, it should provide evidence. The margin of error applies here, too. But even if it is true that voters are more likely to judge Harris as liberal than to judge Trump as conservative, why would this be a risk for Harris?

The Times continues, "For now, [Harris] is edging ahead of [Trump] among critical independent voters." Evidence?

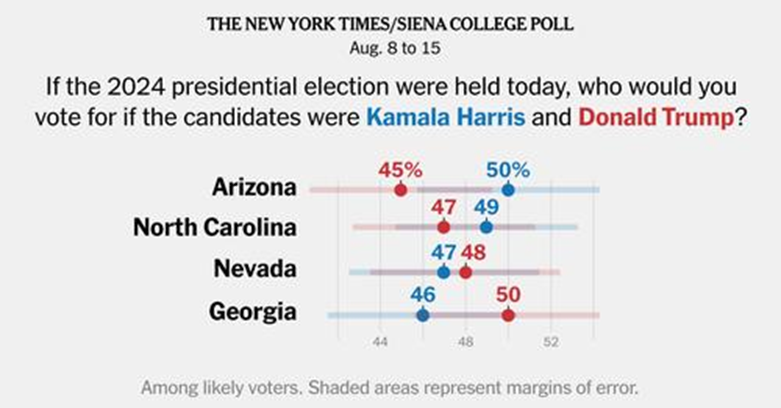
The Times also writes, "Mr. Trump and Ms. Harris are tied at 48 percent across an average of the four Sun Belt states in surveys conducted Aug. 8 to 15. That marks a significant improvement for Democrats compared with May, when Mr. Trump led Mr. Biden 50 percent to 41 percent across Arizona, Georgia, and Nevada in the previous set of Times/Siena Sun Belt polls, which did not include North Carolina." 

The Times is comparing apples to oranges. One sample includes North Carolina, the other doesn't. And it is not clear why it bothers to make this top-level comparison. The polls differ from state to state, and The Times has specific information about each. Why not stick to reporting the results for each state poll rather than aggregate them into an inferior measure? 

If The Times simply must have a nation-level conclusion, it can view each state poll as an observation in a sample of all state polls and compute the probability that Harris is leading nationwide, given the sample of state polls. Do the same for May.

Finally, a puzzle. In Arizona, The Times/Siena poll reports Harris ahead in the sample by 5% among likely voters and 4% among registered voters. But the poll by the Competitiveness Coalition/Public Opinion Strategies about two weeks earlier reported Trump ahead by 5% among likely voters. And The Hill/Emerson College poll about three weeks before The Times/Siena poll reported Trump ahead among registered voters by 5%. Were these differences due to Harris's momentum? Or were they due to differences in how the polls were conducted?

 

                                           Source: The New York Times

 The key question: Are The Washington Post and The New York Times statistically significant? 

Anyway, these conundrums pertain to Central Asia because the political polling in the region, or at least the reporting of it, is anything but perfect. The margin of error is correspondingly higher.  In short, politics pervade political statistics. --Leon Taylor, Seymour, Indiana, tayloralmaty@gmail.com 

 

Notes             

For helpful comments, I thank but do not implicate Annabel Benson, Richard Green, and Mark Kennet. Parts of this post draw upon my earlier articles on my Facebook page.

 

References

Dan Balz, Scott Clement, and Emily Guskin.  Kamala Harris holds slight national lead over Donald Trump, Post-ABC-Ipsos poll finds - The Washington Post August 18, 2024.

Shane Goldmacher and Ruth Igielnik.  Kamala Harris Puts Four Sun Belt States Back in Play, Times/Siena Polls Find - The New York Times (nytimes.com)  August 17, 2024.

Lisa Lerer and Ruth Igielnik.  Harris Leads Trump in Three Key States, Times/Siena Polls Find - The New York Times (nytimes.com)  August 10, 2024.